扫描二维码下载APP



扫描二维码下载APP



扫描二维码下载APP




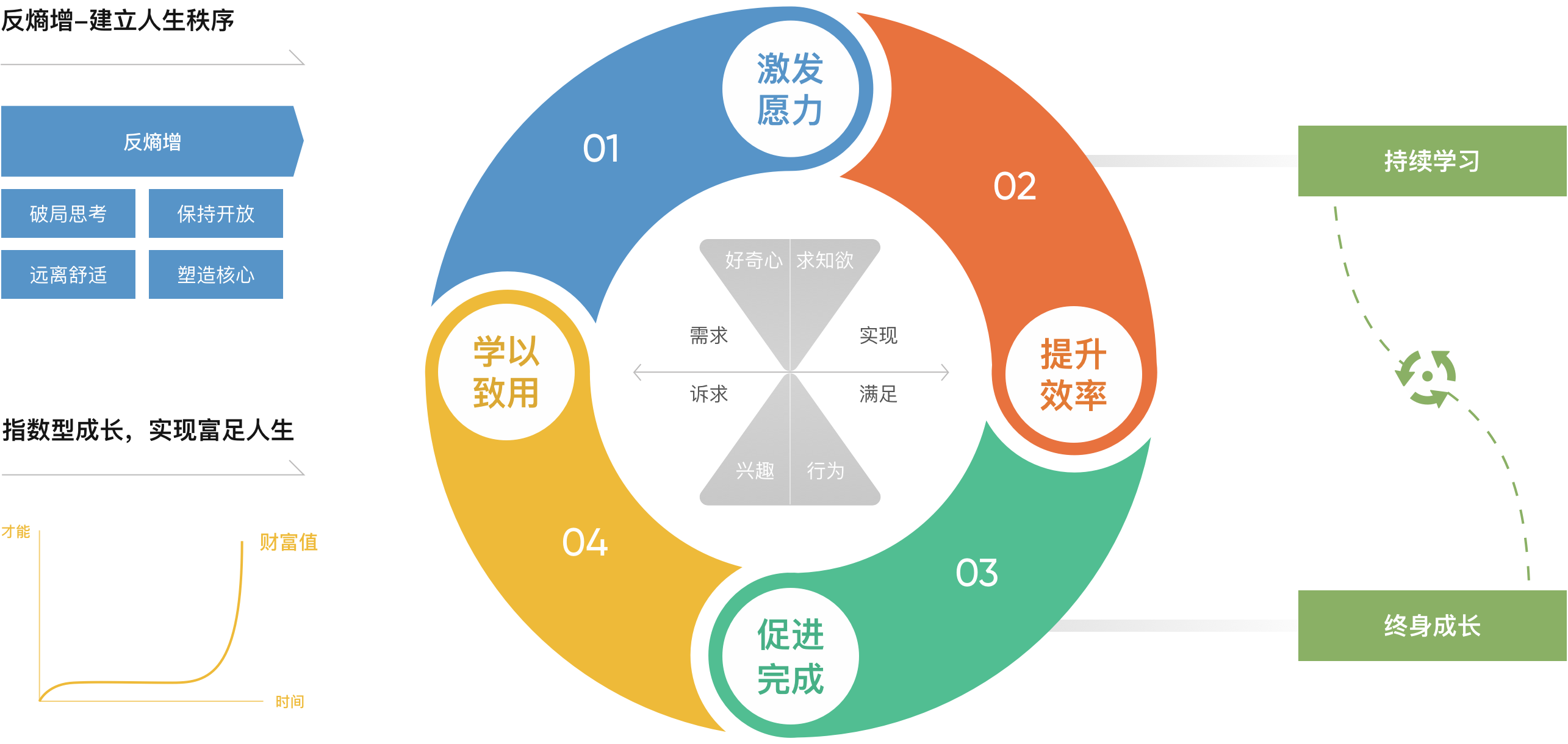

连接用户与内容
覆盖所有主流自媒体渠道 已汇聚6000万粉丝

有书

国学一刻

英语共读

有书少年

轻读实验室

大人修炼手册
连接知识与服务
科学个性化服务体系 助力成长加速

听书

共读

书单

精读

精品课

训练营

直播课
连接文化与生活
线下沉浸式阅读体验 让学习场景触手可及

有书空间

助力 6000万+
书友终身成长

全国 160+
线下同城共读会

传播力超 99%
有书新媒体矩阵

联合 1000+
头部IP

发布 1000+
精选好课

汇聚 500+
顶尖名师

终身教育服务平台
持续的资源积累
打造具有影响力的终身教育服务平台


和千万书友一起成长


艾力
精通六门语言《奇葩说》超人气选手

更多的书籍。更好的自己,更大的世界。

周小鹏
婚恋专家

成长和陪伴是家庭生活最美的风景。

袁文魁
世界记忆大师、《最强大脑》金牌教练

为大脑赋能,让生命绽放!

马丁
知名主持人、媒体评论员

阅读,让人摆脱平庸,实现人生进阶。

申一帆
《最强大脑》人气选手

好的学习能力会受益终生,好的记忆能力为学习加速。

周濂
中国人民大学哲学院教授

怕什么真理无穷,进一寸有一寸的喜欢;惧什么人生有涯,学一天有一天的收获。



查看更多


查看更多
NaN-NaN-NaN
查看详情


荣誉认可打造终身教育行业标杆


市场合作:pr@youshu.cc
广告相关:lizejun@youshu.cc
内容相关:tougao@youshu.cc